Population Algorithm (Semeion©)
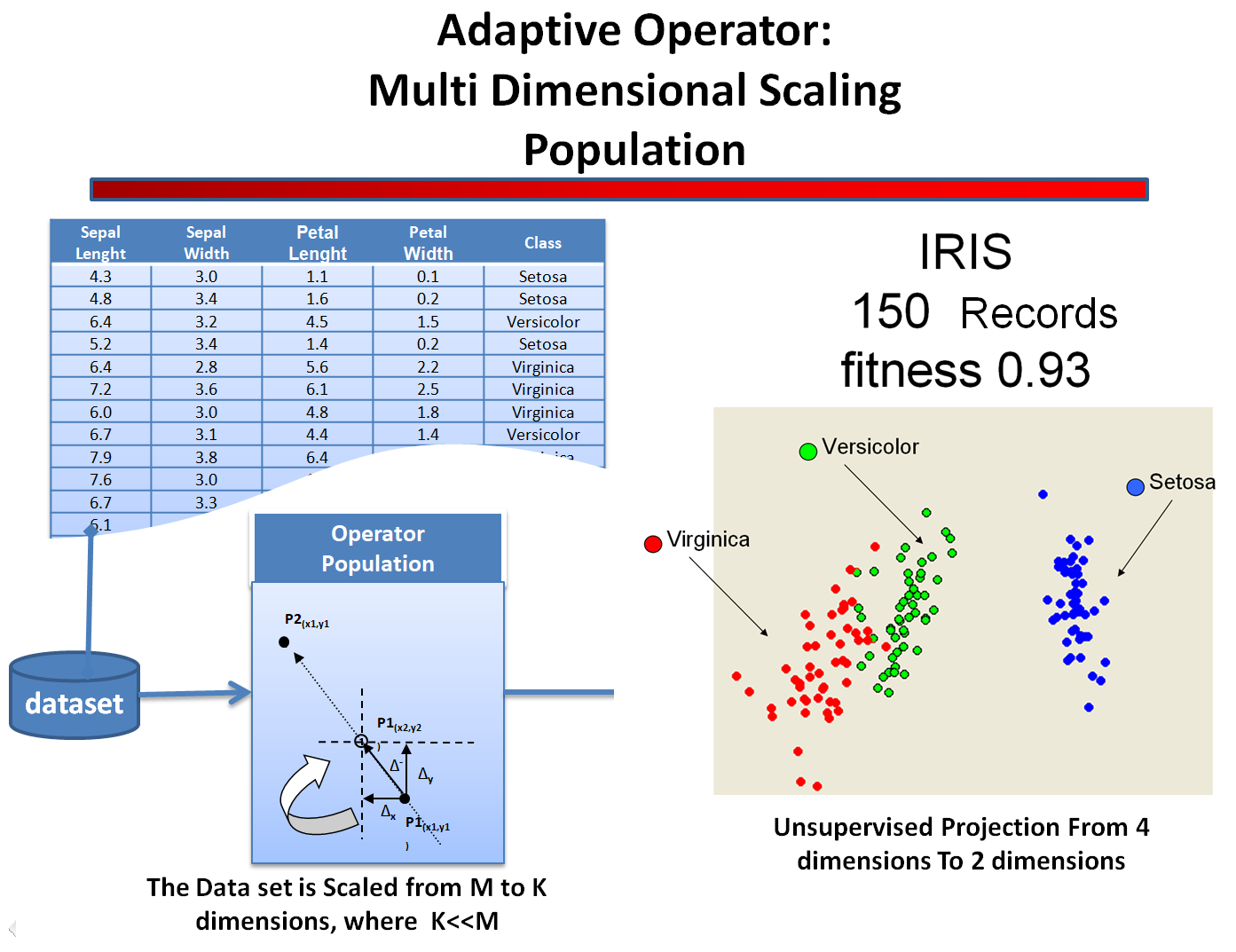
The Population Algorithm (hereafter referred to as Population) has a place in the theoretical framework of Multi Dimensional Scaling. Reducing the dimensionality of a dataset is a frequent problem in the analysis of data and is remarkable important, in particular, in the field of exploratory analysis. Population provides an opportunity to compress N records of a M-dimensional space (which we call the Source Space) in a subspace of Q dimensions (called the Projected Space), where Q<<M, maintaining the greatest possible number of existing relations contained in the original N records. Population is an iterative algorithm based on the calculation of a local fitness, the distance between two points that is considered optimal when the single differences between the matrix of the distances of the Source Space and the matrix of the distances of Projected Space are near zero.
This particular characteristic of Population, the ability to converge on a solution without calculating the global fitness, determines the speed with which it finds a solution minimizing the global error compared to other algorithms of Multi Dimensional Scaling, such as that of Sammon’s map. It is therefore particularly useful for elaborations of datasets of great dimensionality.
The Population program has demonstrated that it possesses a much higher quality for the resolution of the Multi Dimensional Scaling problem. The potential for this algorithm is considerable:
- Speed enhancement;
- Efficiency improvement;
- Simplicity of the algorithm;
- Freedom from having to calculate a specific cost function;
- The possibility of analyzing a dataset of great dimension;
- The possibility of dynamically introducing new records into the dataset during the program run;
- The possibility of choosing the dimensions of Projected Space.
References
[1] Giulia Massini, Stefano Terzi, Paolo Massimo Buscema
Population Algorithm: A New Method of Multi-Dimensional Scaling
Chapter 3, pp 63-74, in W.J. Tastle (ed.), Data Mining Applications Using Artificial Adaptive Systems, DOI 10.1007/978-1-4614-4223-3_1, Springer Science+Business Media New York 2013